Thuật toán Metropolis-Hastings là một thuật toán sinh ra số giả ngẫu nhiên hội tụ đến phân phối dừng của một chuỗi Markov. Nó được sử dụng rộng rãi trong mô phỏng ngẫu nhiên, đặc biệt trong thống kê, thống kê vật lý.

Thuật toán Metropolis-Hastings: Giả sử ta cần sinh một mẫu ngẫu nhiên của quá trình Markov \(X_0,X_1,...\) có phân phối dừng là \(f(x)\) (hàm mục tiêu). Thuật toán được thực hiện qua các bước sau

- Đề xuất một phân phối (phù hợp) \(g(\cdot| X_t)\);

- Sinh \(X_0\) từ phân phối \(g\);

- Lặp lại (cho đến khi dãy hội tụ đến phân phối dừng theo một tiêu chuẩn nào đó):

                 + Sinh \(Y\) từ \(g(\cdot| X_t)\),

                 + Sinh \(U\) từ phân phối đều U\((0,1)\),

                 + Nếu $$U \leq \dfrac{f(Y)g(X_t|Y)}{f(X_t)g(Y|X_t)}$$ ta chấp nhận \(Y\) và đặt \(X_{t+1}=Y\); nếu không ta đặt \(X_{t+1}=X_t\);

Quan sát rằng đối tượng \(Y\) được chấp nhận với xác suất $$\alpha(X_t, Y)=\min\left(1,\dfrac{f(Y)g(X_t|Y)}{f(X_t)g(Y|X_t)}\right)$$

Ví dụ: Sinh mẫu ngẫu nhiên từ phân phối mũ \(\pi(x) = \exp(-x)\) với \(x \geq 0\). Sau đây là Histogram từ mẫu được sinh ra (10000 giá trị) so với giá trị thực của phân phối (đường liền nét).

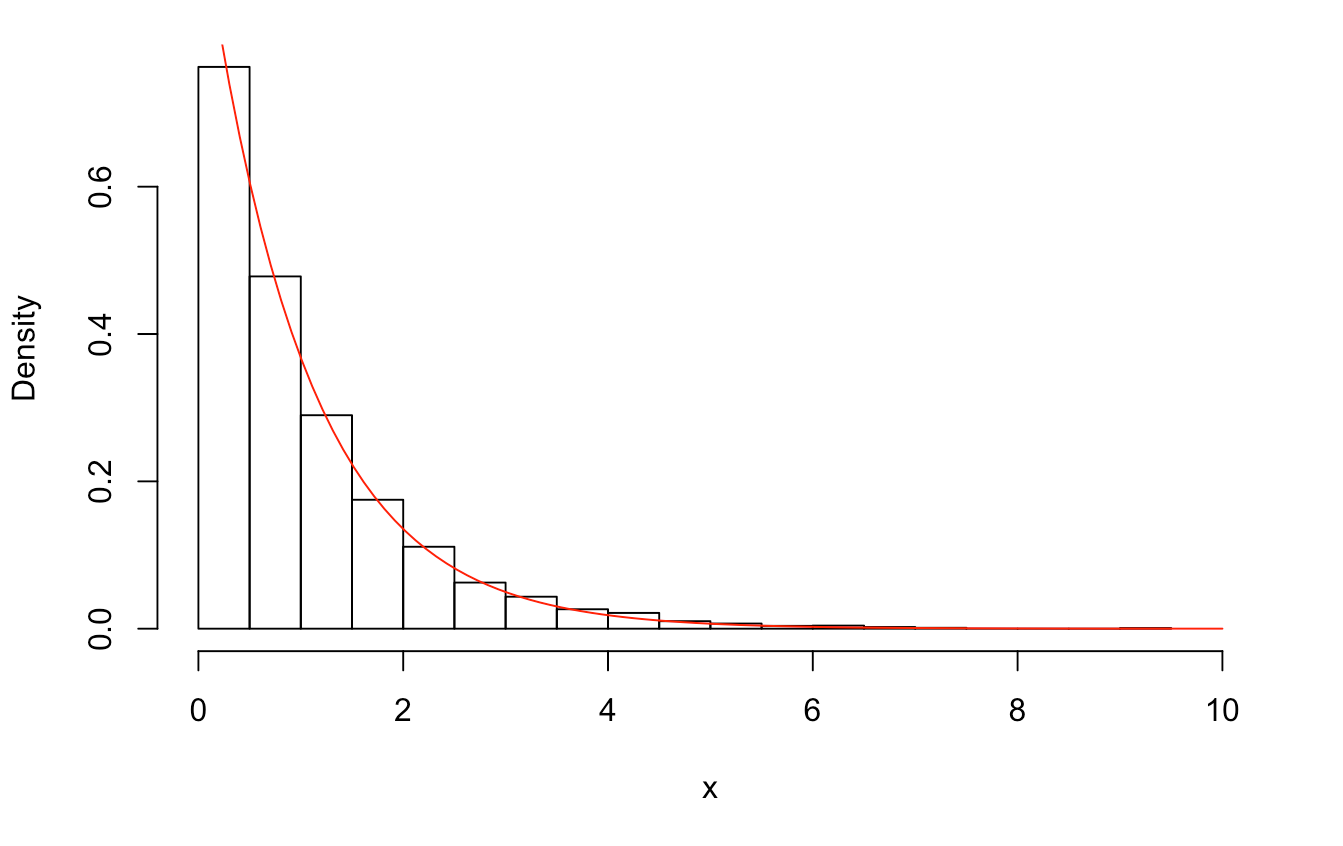
Nhận xét: Histogram của mẫu sinh ra bởi phương pháp Metropolis-Hastings  rất gần (fit) với phân phối mũ.

Tài liệu tham khảo: Christian Robert, George Casella, Introducing Monte Carlo Methods with R, Springer, 2010.

» Tin mới nhất:

• CÁC NGUYÊN TẮC SƯ PHẠM VÀ PHƯƠNG PHÁP DẠY HỌC CHỦ YẾU ĐƯỢC SỬ DỤNG TRONG GIẢNG DẠY CHẤT HỮU CƠ - PHẦN: HYDROCACBON NO (tiếp theo) (18/07/2022)
• Tính các giá trị thống kê thực nghiệm bằng phần mềm Excel (11/07/2022)
• Ước lượng cho phương sai của tổng thể bằng Minitab (19/06/2022)
• CÁC HIỆN TƯỢNG ĐẶC BIỆT CỦA ĐIỆN TỬ TRONG BÁN DẪN III-V (19/06/2022)
• CÁC NGUYÊN TẮC SƯ PHẠM VÀ PHƯƠNG PHÁP DẠY HỌC CHỦ YẾU ĐƯỢC SỬ DỤNG TRONG GIẢNG DẠY CHẤT HỮU CƠ - PHẦN: HYDROCACBON NO (tiếp theo) (18/06/2022)

» Các tin khác:

• CÁC NGUYÊN TẮC SƯ PHẠM VÀ PHƯƠNG PHÁP DẠY HỌC CHỦ YẾU ĐƯỢC SỬ DỤNG TRONG GIẢNG DẠY CHẤT HỮU CƠ - PHẦN: HYDROCARBON NO (17/05/2022)
• Nghiên cứu ứng dụng phần mềm Minitab trong Phân phối nhị thức (18/04/2022)
• CƠ CHẾ ĐIỆN TRỞ VI PHÂN ÂM (18/04/2022)
• CÁC NGUYÊN TẮC SƯ PHẠM VÀ PHƯƠNG PHÁP DẠY HỌC CHỦ YẾU ĐƯỢC SỬ DỤNG TRONG GIẢNG DẠY CHẤT HỮU CƠ - PHẦN: CƠ CHẾ PHẢN ỨNG HỮU CƠ (tiếp theo) (18/04/2022)
• Hệ số tương quan tuyến tính (Hệ số tương quan Pearson) (18/03/2022)
• CÁC NGUYÊN TẮC SƯ PHẠM VÀ PHƯƠNG PHÁP DẠY HỌC CHỦ YẾU ĐƯỢC SỬ DỤNG TRONG GIẢNG DẠY CHẤT HỮU CƠ - PHẦN: CƠ CHẾ PHẢN ỨNG HỮU CƠ (18/03/2022)
• Tính các giá trị thống kê thực nghiệm bằng phần mềm Excel (18/03/2022)
• HƯƠNG CAM (18/01/2022)
• Sơ lược chứng minh Định lý giới hạn trung tâm bằng phương pháp Stein (18/01/2022)
• CÁC NGUYÊN TẮC SƯ PHẠM VÀ PHƯƠNG PHÁP DẠY HỌC CHỦ YẾU ĐƯỢC SỬ DỤNG TRONG GIẢNG DẠY CHẤT HỮU CƠ - PHẦN: PHÂN LOẠI PHẢN ỨNG HỮU CƠ (17/01/2022)