Ở bài viết trước chúng tôi đã giới thiệu Thuật toán Metropolis-Hastings để sinh ra số giả ngẫu nhiên của một phân phối cho trước. Xem ở đây Thuật toán Metropolis-Hastings.

Trong bài viết này chúng tôi sẽ xét một trường hợp riêng của thuật toán trên được gọi là Thuật toán Metropolis-Hastings độc lập. Cụ thể thuật toán như sau

- Phân phôí đề xuất \(g\) độc lập với giá trị trước đó của xích Markov. Cụ thể như sau \[g(Y|X_t) = g(Y)\].

- Xác xuất chấp nhận trong trường hợp này là

\[\alpha(X_t,Y) =\min \left(1, \dfrac{f(Y)g(X_t)}{f(X_t)g(Y)}\right); \]

Ví dụ: Mô phỏng đại lượng ngẫu nhiên \(X\) phân phối mũ \(Exp(1)\). Hàm mật độ của \(X\) có dạng như sau

\[f(x) = e^{-x},\ \ x \geq 0.\]

- Ta chọn phân phối đề xuất là \(Exp(\lambda)\) có hàm mật độ

\[g(x) = \lambda e^{-\lambda x},\ \ x \geq 0.\]

- Xác xuất chấp nhận trong trường hợp này là \[\alpha(x,y) = \min\{1, \exp\{(1-\lambda)(x-y)\}\}\].

Xem dưới đây là hai mô phỏng cho phân phối mũ \(Exp(1)\) với hai lựa chọ cho giá trị \(\lambda\): 0.2 (hình trên) và 1.5 (hình dưới).

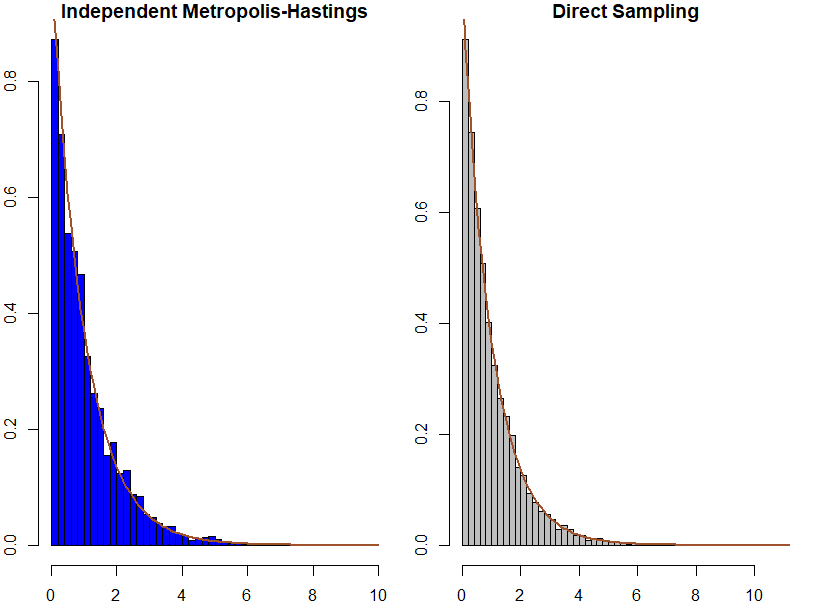
Mô phỏng ngẫu nhiên cho phân phối mũ \(Exp(1)\) với hai lựa chọ cho giá trị \(\lambda\): 0.2 

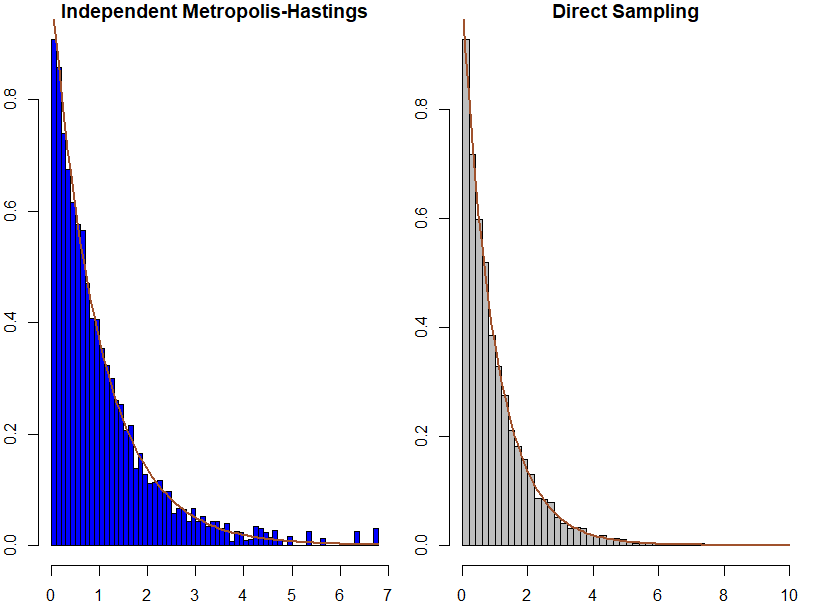
Mô phỏng ngẫu nhiên cho phân phối mũ \(Exp(1)\) với hai lựa chọ cho giá trị \(\lambda\): 1.5

Tài liệu tham khảo: Christian Robert, George Casella, Introducing Monte Carlo Methods with R, Springer, 2010.

» Tin mới nhất:

• CÁC NGUYÊN TẮC SƯ PHẠM VÀ PHƯƠNG PHÁP DẠY HỌC CHỦ YẾU ĐƯỢC SỬ DỤNG TRONG GIẢNG DẠY CHẤT HỮU CƠ - PHẦN: HYDROCACBON NO (tiếp theo) (18/07/2022)
• Tính các giá trị thống kê thực nghiệm bằng phần mềm Excel (11/07/2022)
• Ước lượng cho phương sai của tổng thể bằng Minitab (19/06/2022)
• CÁC HIỆN TƯỢNG ĐẶC BIỆT CỦA ĐIỆN TỬ TRONG BÁN DẪN III-V (19/06/2022)
• CÁC NGUYÊN TẮC SƯ PHẠM VÀ PHƯƠNG PHÁP DẠY HỌC CHỦ YẾU ĐƯỢC SỬ DỤNG TRONG GIẢNG DẠY CHẤT HỮU CƠ - PHẦN: HYDROCACBON NO (tiếp theo) (18/06/2022)

» Các tin khác:

• ƯỚC LƯỢNG KHOẢNG CHO GIÁ TRỊ TRUNG BÌNH BẰNG MINITAB (18/05/2022)
• Thuật toán Metropolis-Hastings (18/05/2022)
• CÁC NGUYÊN TẮC SƯ PHẠM VÀ PHƯƠNG PHÁP DẠY HỌC CHỦ YẾU ĐƯỢC SỬ DỤNG TRONG GIẢNG DẠY CHẤT HỮU CƠ - PHẦN: HYDROCARBON NO (17/05/2022)
• Nghiên cứu ứng dụng phần mềm Minitab trong Phân phối nhị thức (18/04/2022)
• CƠ CHẾ ĐIỆN TRỞ VI PHÂN ÂM (18/04/2022)
• CÁC NGUYÊN TẮC SƯ PHẠM VÀ PHƯƠNG PHÁP DẠY HỌC CHỦ YẾU ĐƯỢC SỬ DỤNG TRONG GIẢNG DẠY CHẤT HỮU CƠ - PHẦN: CƠ CHẾ PHẢN ỨNG HỮU CƠ (tiếp theo) (18/04/2022)
• Hệ số tương quan tuyến tính (Hệ số tương quan Pearson) (18/03/2022)
• CÁC NGUYÊN TẮC SƯ PHẠM VÀ PHƯƠNG PHÁP DẠY HỌC CHỦ YẾU ĐƯỢC SỬ DỤNG TRONG GIẢNG DẠY CHẤT HỮU CƠ - PHẦN: CƠ CHẾ PHẢN ỨNG HỮU CƠ (18/03/2022)
• Tính các giá trị thống kê thực nghiệm bằng phần mềm Excel (18/03/2022)
• HƯƠNG CAM (18/01/2022)