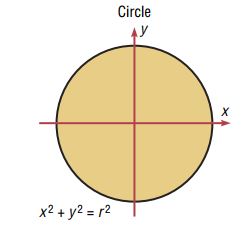
Trong toán học, các đường cong có thể được biểu diễn bằng các phương trình. Ví dụ: Đường tròn trong hình trên được biểu diễn bởi phương trình:\[ x^2 +y^2= r^2, \]trong đó r là bán kính. Một đường tròn có thể được sử dụng để đại diện cho nhiều đối tượng vật lý, chẳng hạn như bánh xe hoặc bánh răng. Mặc dù không thể chế tạo một bánh xe tròn hoàn hảo, phương trình và tính chất của một đường tròn có thể được sử dụng để nghiên cứu nhiều khía cạnh của bánh xe, chẳng hạn như diện tích, vận tốc và gia tốc. Theo cách tương tự, đường cong phân phối chuẩn cũng được biễu diễn bằng một phương trình và đường cong phân phối chuẩn cũng có thể được sử dụng để nghiên cứu nhiều biến không được hoàn hảo phân phối chuẩn nhưng xấp xỉ phân phối chuẩn. Phương trình toán học cho phân phối chuẩn là:

Biến ngẫu nhiên \(X\) được gọi là tuân theo luật phân phối chuẩn, kí hiệu \(X\sim N(\mu,\sigma)\), nếu hàm mật độ xác suất của \(X\) có dạng: $$f(x)=\dfrac{1}{\sigma\sqrt{2\pi}}e^{-\dfrac{(x-\mu)^2}{2\sigma^2}},$$ trong đó:
\(X \) là các giá trị của \(X\);
\(e\approx 2.718\);
\(\pi\approx 3.14\);
\(\mu\): trung bình của tổng thể;
\(\sigma\):  độ lệch chuẩn của tổng thể.

Các dạng đồ thị của phương trình đường phân phối chuẩn:

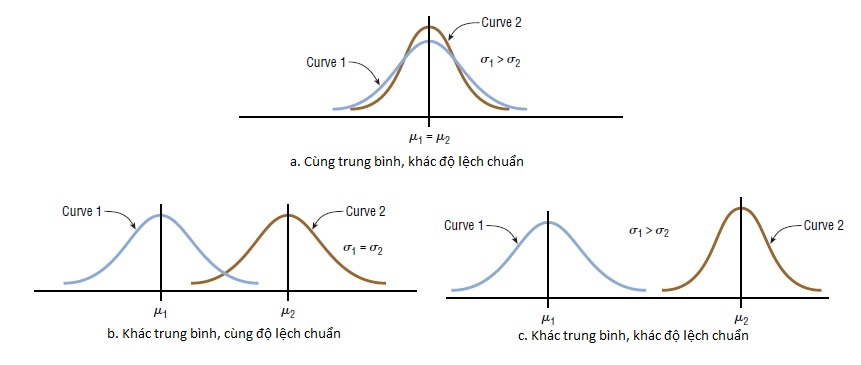
Một phân phối chuẩn có các tính chất sau:

-Đồ thị của phân phối chuẩn có dạng hình chuông.
-Trung bình, trung vị và mode đều bằng nhau và nằm ở trung tâm của phân bố.
- Phân phối chuẩn là một đường cong chỉ có một mode duy nhất.
- Đồ thị là một đường cong đối xứng qua đường thẳng đứng đi qua trung bình.
- Là một đường cong liên tục.
- Là đường cong nhận trục \(Ox\) làm tiệm cận ngang.
- Tổng diện tích phần phía dưới đường cong phân phối chuẩn luôn bằng 1. Diện tích nằm dưới đường cong phân phối chuẩn nằm trong khoảng 1 độ lệch chuẩn là xấp xỉ \(0.68\); trong khoảng 2 độ lệch chuẩn khoảng \(0.95\) và trong khoảng 3 độ lệch chuẩn khoảng \(0.997\).

Phân phối chuẩn tắc (standard normal distribution)

Mỗi phân phối chuẩn được đặc trưng bởi trung bình \(\mu\) và độ lệch chuẩn \(\sigma\) của nó . Như vậy có vô số phân phối chuẩn với hình dáng và vị trí khác nhau, trong số đó có một phân phối đặc biệt hơn hết đó là phân phối chuẩn tắc.
Phân phối chuẩn tắc là phân phối chuẩn với trung bình bằng 0 và độ lệch chuẩn bằng 1.
Khi đó hàm số cho phân phối chuẩn tắc là: $$f(z)=\dfrac{1}{\sqrt{2\pi}}e^{-\dfrac{z^2}{2}}$$
Tất cả các biến phân phối chuẩn có thể được biến đổi thành biến phân phối chuẩn tắc bằng cách sử dụng công thức cho điểm chuẩn (\(z\)-core): $$z=\dfrac{X-\mu}{\sigma}.$$